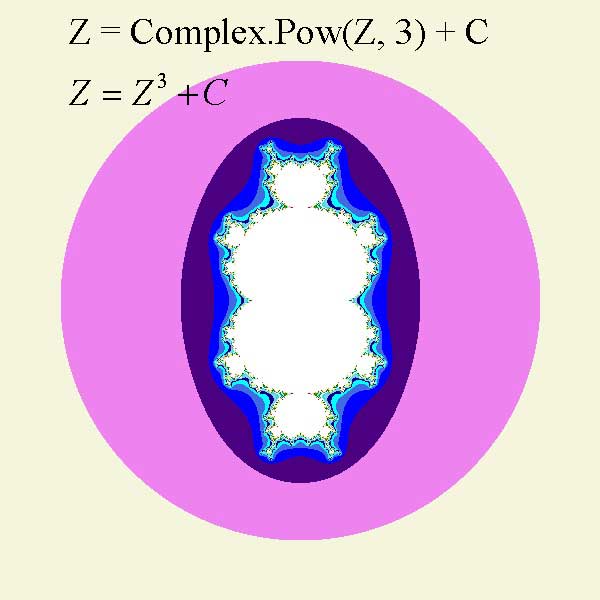
Il frattale di
Mandelbrot.
Nella fine del secolo scorso
il matematico polacco Beinot Mandelbrot lavorando con i calcolatori della IBM
ideò e studiò una curiosa figura geometrica piana frattale che prese il suo
nome.
Il concetto è abbastanza
semplice: consideriamo il piano immaginario che rappresenta graficamente
l’insieme dei numeri complessi ovvero un quadro di lato L composto dai pixel di
una finestra del video. Può essere pensato come un piano cartesiano modificato,
con la parte reale rappresentata sull'asse x e la parte immaginaria rappresentata sull'asse
y.L'asse x è
chiamato anche l'asse reale e l'asse y asse immaginario.
Associamo ad ogni punto del piano immaginario (ovvero ad ogni pixel della
finestra) un colore che ricaveremo applicando alle coordinate di ciascun punto
una certa funzione ricorsiva (condizionata da alcune regole). Facendo questa
operazione per tutti i punti (o pixel) del quadro coloreremo tutta la finestra.
Le coordinate di un punto A
generico del piano siano x ed y ; associamo a questo
punto il numero complesso Z = x+jy .
Ora consideriamo una
successione di numeri complessi che si ottiene dalla relazione
:
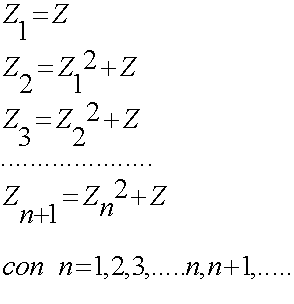
Perciò ad ogni elemento complesso della
successione
Vediamo con alcuni esempi
numerici come evolvono le successioni relativamente a vari punti del piano
immaginario. Partiamo da un punto B di coordinate x=1, y = 1
B1(1,1) → B2(1,3)
→ B3(-7,7) → B4(1,-97) → B5(-9407,-193)
→ …. ;
Difatti per ottenere la
coordinate di B2 applichiamo la formula di Mandelbrot al
punto B1, cioè:
(1 + j 1)2 + (1 + j
1) = 1 +2 j – 1 +1 + j = 1 + 3 j
Il punto successivo B3 si
otterrà ancora con la stessa formula applicata al punto B2, ovvero:
(1 + 3 j)2 + ( 1 + j) = ( 1 + 6 j – 9) + (1 + j ) = -7 +7 j
E così via ….
Altri punti potrebbero essere:
C1(-1.4 , 0.3) → C2(0.470 ,-0.540) → C3(-1.470
, -0.207) → …C7(-27.437, 11.433)….→….;
D1(0.15 , 0.21) → D2(0.128 , 0.273) →
…→D10(0.092 , 0.257) →…. →D100(0.092 ,0.257) →……;
E1(-0.12 , 0.13) → E2(-0.122 , 0.098) → E3(-0.115
, 0.106) →…. →E10(-0.117 ,
0.105) →…→E100(-0.117 , 0.105) →…;
Si osserva che per alcune di queste successioni di punti(B e C), al crescere di n, i punti si allontanano
sempre di più dall’ origine degli assi, per altre ( D ed E ) i punti finali non
si spostano più.
Si può fare un semplice programma con VB2010 che permette
si calcolare la successione di Mandelbrot indicando punto iniziale e numero di
iterazioni da eseguire .
Si apra un nuovo progetto in VB2010 e in una form si
inseriscano un Button
quattro ListBox tre TextBox e sette Label disponendo il tutto come da figura
sottostante.
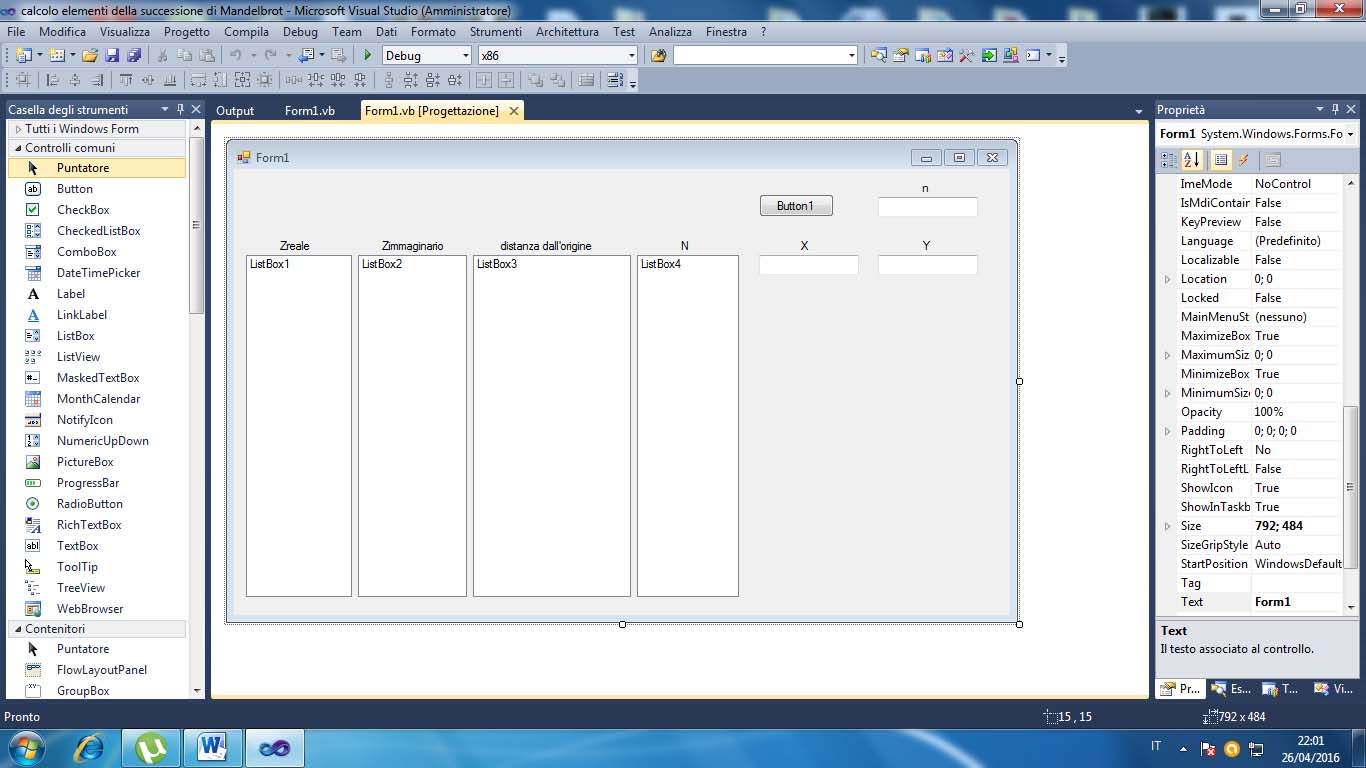
Si scriva il codice seguente
importando la classe System.Numerics che agevola l’esecuzione del calcolo di
numeri complessi.
Questo mezzo per lavorare con
i numeri complessi in VB2010 ci è fornito dal Net.Framework 4 che deve essere
installato nel computer .
CODICE in VB.NET 2010 :
' per importare la classe
System.Numerics nel progetto cliccare sul pulsante "Progetto"
'poi selezionare
'dal menu' a tendina "Aggiungi
riferimento". All' apertura della finestra cliccare su
' ".NET" e scegliere nell'elenco
System.Numerics dando l' OK.
Imports System.Numerics
Public Class Form1
Private Sub Button1_Click(ByVal
sender As System.Object, ByVal e As System.EventArgs) Handles Button1.Click
' definiamo le variabili :
' x,y
sono le coordinate del punto di partenza che scriveremo nei rispettivi textbox
' n corrisponde al numero di iterazioni
ovvero di punti che desideriamo trovare
' C è il punto di partenza
della successione e Z i punti successivi per vari n crescenti
' di una unità.
' Z = Complex.Pow(Z, 2) + C
è la formula ricorsiva di Mandelbrot che verrà aggiornata
'per ogni ciclo.
Dim x, y As
Double
Dim n, v As Integer
x
= TextBox1.Text
y
= TextBox2.Text
n
= TextBox3.Text
Dim Z0 As
New Numerics.Complex(x, y)
Dim Z As New Numerics.Complex(0,
0)
For v = 1 To n Step
1
Z = Complex.Pow(Z,
2) +Z0
' usando la classe Numerics
in VB.NET è facile risalire alla parte reale o immaginaria di un
' numero complesso con la
notazione Z.Real o Z. Imaginary rispettivamente. Esse vengono
' visualizzate per ogni
ciclo for nelle rispettive ListBox.
ListBox1.Items.Add(Z.Real)
ListBox2.Items.Add(Z.Imaginary)
' per il teorema di Pitagora
il modulo o la distanza dall'origine di un numero complesso
' si ottiene eseguendo la
radice quadrata della somma dei quadrati di parte reale e parte
'immaginaria.
' Tale valore finisce
scritto nella ListBox3
ListBox3.Items.Add(Math.Sqrt(Z.Real ^ 2 + Z.Imaginary
^ 2))
ListBox4.Items.Add(v)
Next
End Sub
End Class
FINE DEL CODICE in VB:NET2010
Con il programmino di sopra si
possono verificare i punti già calcolati e trovarne altri.
Si osserva che per alcuni
punti iniziali c’è un rapido allontanamento della successione di punti dall’origine,
mentre per altri, per quanti termini avanzi la successione i corrispondenti
punti restano sempre nei dintorni dell’origine degli assi O.
C’è una dimostrazione
che afferma che se i punti
iniziali della successione sono al di fuori del cerchio di centro O (origine
assi) e raggio 2, nominato cerchio critico, col procedere dei passi della
successione relativa, i punti corrispondenti si allontaneranno sempre di più
dall’ origine.
Se invece i punti di partenza
sono interni al cerchio critico non è possibile prevedere se le relative
successioni procederanno portando i punti associati fuori dal cerchio critico
dopo 1,2,..n passi oppure non ne usciranno mai anche
dopo infiniti passi.
Da questi presupposti andiamo
a colorare i punti iniziali del piano immaginario per ottenere la figura di
Mandelbrot
Stabiliamo innanzitutto che
sia N il numero
massimo di passi (che per il computer dovrà essere un numero intero finito) per
l’avanzamento delle successioni relative a tutti i punti del piano cartesiano
(del quadro di lato L) e che si disponga
di una tavolozza con lo stesso numero di colori diversi numerati ordinatamente
da 0 a N
Per ogni punto iniziale potremmo
trovare un numero di passi n della successione per cui si verifica che il punto
corrispondente esce oppure no dal cerchio di raggio critico. Per quelli che non
escono dal cerchio dopo N passi supporemo che non
escano mai e ai relativi punti iniziali assoceremo il colore N. Se invece dopo n passi di avanzamento
della successione (1,2, …10,…ecc.) troveremo un punto
corrispondente che esce per primo dal cerchio critico assoceremo al punto
iniziale il colore n.
Per punti esterni al cerchio
critico associamo il colore 0,(perché già dal passo 0
siamo esterni al cerchio critico e perché sappiamo che la successione si
allontanerà sempre più da esso) che è anche il colore di sfondo ( ad esempio il
marrone)
Ovviamente la figura di
Mandelbrot si svilupperà maggiormente intorno al cerchio critico di raggio 2
per cui prenderemo un quadro di lato L in modo che -2,5<=
x<=+2,5 ed -2,5<=y<=+2,5.
Lavorando con un video e con
VB.net si ha a che fare con i pixel di una Picture Box che potremmo
scegliere di 600x600 pixel su cui disegnare la figura di Mandelbrot.Nell’esempio
riportato sotto, considerando che le coordinate della pictureBox partono dallo
spigolo in alto a sinistra della medesima, occorre fare corrispondere i punti del dominio e codominio
della funzione di Mandelbrot ( che sono quegli insiemi indicati prima) con
quelli della picturebox.
Questo si ottiene per le
coodinate dell’ asse x
(ovvero la parte reale del punto) con la funzione in Vb.net “ calcolaparterealeX “ che prende un
qualunque valore intero X pixel (compreso tra 0 e 599) ne calcola il rapporto f con il lato L in
pixel della picturebox ( f = x /600) lo moltiplica per la larghezza del domino
della funzione di Mandelbrot (5) ed
infine sottrae il risultato alla metà del dominio (che è 2,5 ) . E’così che si
trova il criterio per la corrispondenza tra i punti (in decimale) del piano
cartesiano dove si implementa la successione complessa di Mandelbrot con i
pixel (x variabile Integer)
della Picturebox da colorare..
Ad esempio il punto X della picture box
di ascissa 300 pixel (che divide la picturebox a metà) verrà riportato sul
piano cartesiano della funzione di Mandelbrot alla coordinata x =
(300/600)*5-2,5 = 0 verificando così la similitudine tra punti
dei due piani.
Analogamente la funzione
VB.Net “calcolaparteimgY “ permette di associare le
ordinate della picture box con i punti dell’ asse immaginario (o asse y) del
piano .
In pratica, si fa eseguire
al programma un cambio di coordinate in modo da disporre la figura al centro
del quadro.
La classe System. Numerics in
VB.NET permette di lavorare abbastanza agevolmente con i numeri complessi
eseguendo calcoli su questi tramite alcune istruzioni.
Istruzioni che si utilizzano
nel programma per trovare i valori della successione di Mandelbrot e per
determinare il modulo di un numero complesso ovvero nel nostro caso la distanza
del punto corrispondente dall’origine. Il programma verificherà poi il numero
di passi che necessitano affichè si abbia o meno l’uscita dei punti associati
alla successione dal cerchio di raggio 2 e colorerà il punto di partenza di
conseguenza. ' NB:occorre importare la classe System.Numerics dal menu'
principale cliccando su Project--->Add Reference, e quindi 'selezionare .NET per
cliccare la scelta 'System.Numerics' e confermare con OK. SOLO così si importa
tale classe nel progetto 'che si
desidera realizzare. Imports System.Numerics Public Class Form1 Private Sub Form1_Load(ByVal sender As System.Object,
ByVal e As System.EventArgs)
Handles MyBase.Load Me.Size = New Size(800, 788) End Sub Private Sub Button1_Click(ByVal sender As System.Object,
ByVal e As System.EventArgs)
Handles Button1.Click Button1.Hide() Dim Raggio
As Integer = 2 Dim BmpLarg
As Integer = 600 Dim BmpAlt
As Integer = 600 Dim MaxCicli
As Integer = 27 Dim RealAsseLungh
As Decimal = 5D Dim RealAsseValMin
As Decimal = -2.5D Dim ImgAsseLungh
As Decimal = 5D Dim ImgAsseValMin
As Decimal = -2.5D Dim BMP As New Bitmap(BmpLarg, BmpAlt) For x As Integer = 0
To BmpLarg - 1 For y As Integer = 0
To BmpAlt - 1 Dim zReal
As Decimal = CalcolaParteRealeX(x, BmpLarg, RealAsseValMin, RealAsseLungh) Dim zImg
As Decimal = CalcolaParteImgY(y, BmpAlt, ImgAsseValMin, ImgAsseLungh) Dim Z0 As New Numerics.Complex(zReal, zImg) Dim Z As New Numerics.Complex(0, 0) Dim conta
As Integer = 0 For conta
= 0 To 26 Z = (Complex.Pow(Z, 2) + Z0) If (Z.Real
^ 2 + Z.Imaginary ^ 2 >= Raggio
^ 2) Then Exit For Else End If Next Dim PixelColor
As Color If conta
= MaxCicli Then PixelColor = Color.Transparent Else PixelColor =
MappaColori(conta) conta = conta + 1 End If BMP.SetPixel(x,
y, PixelColor) Next Next PictureBox1.Image = BMP 'con la
riga seguente si salva l'immagine dal nome cip in una cartella MANDELBROT (da creare
prima dell'esecuzine dell'app.) nel percorso specificato.Occorre creare questa cartella altrimenti il programma si blocca PictureBox1.Image.Save("C:\MANDELBROT\cip.bmp") End Sub Function MappaColori(ByVal conta
As Integer) As Color Select Case conta Case 0 :
Return Color.Beige Case 1 :
Return Color.Violet Case 2 :
Return Color.Indigo Case 3 :
Return Color.Blue Case 4 :
Return Color.RoyalBlue Case 5 :
Return Color.Cyan Case 6 :
Return Color.DarkBlue Case 7 :
Return Color.LightSkyBlue Case 8 :
Return Color.Turquoise Case 10 :
Return Color.DarkCyan Case 11 :
Return Color.Aquamarine Case 9 :
Return Color.Azure Case 12 :
Return Color.DarkGreen Case 13 :
Return Color.Olive Case 14 :
Return Color.Green Case 15 :
Return Color.LightGreen Case 16 :
Return Color.GreenYellow Case 17 :
Return Color.PapayaWhip Case 18 :
Return Color.LightYellow Case 19 :
Return Color.Yellow Case 20 :
Return Color.Salmon Case 21 :
Return Color.Orange Case 22 :
Return Color.LightPink Case 23 :
Return Color.Purple Case 24 :
Return Color.IndianRed Case 25 :
Return Color.Tomato Case 26 :
Return Color.Red End Select End Function Function CalcolaParteRealeX(ByVal x As Integer, ByVal bitmapLargh
As Integer, ByVal LarghSemiPianoComplesso
As Decimal, ByVal LarghPianoComplesso
As Decimal) As Decimal Dim f As Decimal = CDec(x / bitmapLargh) Dim ParteReale As Decimal = f *
LarghPianoComplesso Return ParteReale +
LarghSemiPianoComplesso End Function Function CalcolaParteImgY(ByVal y As Integer, ByVal bitmapAlt
As Integer, ByVal AltSemiPianoComplesso
As Decimal, ByVal AltPianoComplesso
As Decimal) As Decimal Dim f As Decimal = CDec(y / bitmapAlt) Dim ParteImg
As Decimal = f
* AltPianoComplesso
Return ParteImg +
AltSemiPianoComplesso
End Function Private Sub PictureBox1_Click(ByVal sender As System.Object,
ByVal e As System.EventArgs)
Handles PictureBox1.Click End Sub 'con questa
sub si disegna sulla picturebox1 un cerchio rosso di raggio 2 che si posiziona
utilizzando il quadrato escritto 'di lato
480 pixel e nella posizione x=60,y= 60 pixel per
averlo al centro della picturebox1 di 600x600pixel Private Sub PictureBox1_Paint(ByVal sender As Object, ByVal e As System.Windows.Forms.PaintEventArgs) Handles
PictureBox1.Paint e.Graphics.DrawEllipse(Pens.Red, 60, 60, 480, 480) End Sub End Class FINE CODICE FIGURA MANDELBROT.
Si otterrà una figura di questo tipo dopo
avere avviato il programma e cliccato sul pulsante button :
Utilizzando analogo programmino si possono ottenere altre figure piane colorate, non
Necessariamente riferibili ad un frattale, sotituendo alle righe corrispondenti alla formula
Di mandelbrot altre formule matematiche.
Ad esempio:
In queste formule C è un numero complesso scelto a caso che deforma la figura di Mandelbrot.
Per scaricare il programma zip clicca qui
Per realizzare il programma
si crea un nuovo progetto form in vb2010 e si trascina nell form (800x788 pixel) un button e
una picture box di 600x 600 pixel per poi copiare e incollare il listatoimmagini1 nello spazio della form1
Occorre inoltre creare una cartella di nome MANDELBROT in C/MANDELBROT che serve per
salvare l'immagine in formato .bmp che potremo elaborare o stampare in seguito.
INIZIO CODICE MANDELBROT: